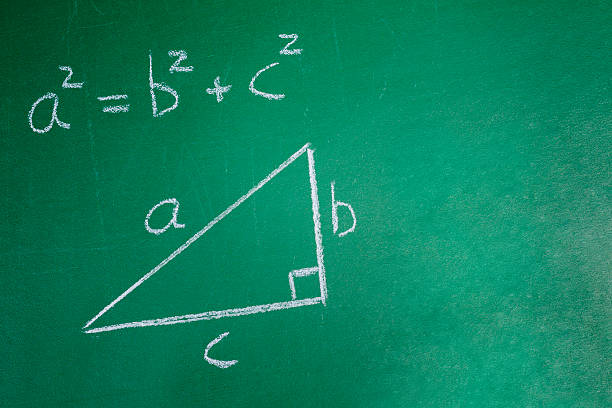
Pisagor Teoremi, geometride oldukça önemli bir yere sahip olan bir teoremdir. Kökeni antik Yunan matematikçisi Pisagor’a dayanan bu teorem, dik üçgenlerle ilgilidir. Pisagor Teoremi’nin formülü, dik kenarların karelerinin toplamının, hipotenüsün karesine eşit olduğunu ifade eder. Bu teorem, geometri problemlerinin çözümünde ve gerçek hayatta birçok alanda kullanılmaktadır. Pisagor Teoremi’nin detaylı tarihçesi, formülü, kullanım alanları ve kanıtlarıyla ilgili bilgilere bu yazımızda yer vereceğiz. Pisagor Teoremi hakkında daha fazla bilgi edinmek için yazımızı okumaya devam edin!
İçerik Tablosu
Pisagor Teoreminin Tarihi
Pisagor Teoremi, Antik Yunan matematikçisi Pisagor’a atfedilir ve M.Ö. 6. yüzyılda ortaya çıkmıştır. Pisagor ve takipçileri, matematik ve geometriye olan katkılarıyla bilinirler. Pisagor, temel olarak doğal sayıları ve geometrik şekilleri inceleyerek, ünlü teoremle ismini matematik tarihine yazdırmıştır. Pisagor Teoremi, dik üçgenlerin kenarlarının karelerinin toplamının hipotenüsün karesine eşit olduğunu ifade eder.
Pisagor’un öğretileri ve teoremi, matematiksel düşünce ve keşiflerde dönüm noktası olmuştur. Onun çalışmaları, bugün modern matematiğin temel taşlarından biri olarak kabul edilir. Pisagor Teoremi’nin tarihi, matematiksel düşünce tarihinde önemli bir dönüm noktası olmuştur ve günümüzde hala matematik eğitiminin temel bir parçasıdır. Pisagor’un teoremi, bugün birçok alanda pratik uygulamalara sahip olmasıyla bilinir. Bu teorem, matematik dünyasında önemli bir yere sahip olmasının yanı sıra, geometri, mühendislik, fizik ve mimarlık gibi alanlarda da kullanılmaktadır. Pisagor Teoremi’nin önemi ve tarihi, matematiğin evrensel bilim olma özelliğini vurgulamaktadır.
Pisagor Teoremi Nedir?
Pisagor Teoremi, üçgenlerin kenarları arasındaki ilişkiyi tanımlayan temel bir geometrik prensiptir. Bu teorem, dik üçgenlerin hipotenüsü (en uzun kenarı) ile diğer iki kenarının uzunlukları arasındaki ilişkiyi ifade eder.
Pisagor Teoremi, şu formülle ifade edilir:
c² = a² + b²
Bu formülde:
- c hipotenüsü,
- a ve b ise dik üçgenin diğer iki kenarlarını temsil eder.
Pisagor Teoremi’nin asıl amacı, dik üçgenlerin geometrik özelliklerini incelemek ve bu üçgenlerin kenarları arasındaki matematiksel ilişkiyi belirlemektir.
Bu teorem, matematikte ve fizikte birçok alanda yaygın kullanılan temel bir prensiptir. Ayrıca, geometri problemlerini çözmek, uzunluk ve mesafe hesaplamaları yapmak gibi birçok pratik uygulama alanı bulunmaktadır.
Pisagor Teoremi’nin anlamı ve kullanımı, geometri ve matematikle ilgilenen herkes için önemlidir. Bu teorem, geometri problemlerini çözmek ve uzunluk hesaplamaları yapmak için vazgeçilmez bir araçtır.
Pisagor Teoremi Formülü
Pisagor Teoremi, dikdörtgen veya eşkenar üçgen gibi belirli üçgen tipleri için geçerlidir. Pisagor Teoremi’nin formülü şu şekildedir:
c² = a² + b²
- c tarafı hipotenüsü temsil eder.
- a ve b ise dik kenarları temsil eder.
Bu formül, bir dik üçgenin hipotenüsünü bulmak için kullanılır. Hipotenüs, dik üçgenin en uzun kenarıdır ve diğer iki kenarın karesinin toplamının karekökü olarak bulunur. Örneğin, eğer a = 3 ve b = 4 ise, hipotenüs (c) = √(3² + 4²) = √(9 + 16) = √25 = 5 olacaktır.
Pisagor Teoremi’nin formülü, dik üçgenlerle ilgili problemleri çözmek için oldukça kullanışlıdır. Ayrıca farklı boyuttaki şekillerin köşelerini doğrulamak için de kullanılabilir. Bu formül, matematikte ve günlük hayatta çeşitli alanlarda kullanılan temel bir teoremdir. Pisagor Teoremi, trigonometri, mühendislik, fizik ve mimarlık gibi birçok alanda önemli bir rol oynamaktadır.
Pisagor Teoreminin Kullanım Alanları
Pisagor Teoremi, geometri ve matematik alanlarında geniş bir kullanım alanına sahiptir. Bu teorem, birçok farklı problem ve durumda pratik bir şekilde kullanılabilir. Pisagor Teoremi’nin başlıca kullanım alanları şunlardır:
Üçgenlerin Özellikleri: Pisagor Teoremi, dik üçgenlerin hipotenüs uzunluğunu bulmada ve üçgenlerin benzerlik durumlarını belirlemede kullanılır.
İnşaat Mühendisliği: İnşaat mühendisliğinde, açılan bir bina inşaatının dik olduğunu kontrol etmek için Pisagor Teoremi kullanılır.
Modelleme ve Haritalama: Harita çizimlerinde ve modelleme işlemlerinde, mesafe hesaplamaları için Pisagor Teoremi sıklıkla kullanılır.
Elektronik ve Bilgisayar Programlama: Devrelerin karmaşıklığını ve bileşenlerin konumlarını belirlemede Pisagor Teoremi’nin formülü kullanılır.
Pisagor Teoremi’nin bu geniş kullanım alanları, matematiksel kavrayışın ve pratik problemlerin çözümünde büyük bir öneme sahiptir. Bu nedenle, teoremin kullanım alanlarını anlamak, farklı disiplinlerdeki profesyoneller için oldukça değerlidir.
Pisagor Teoremi İle İlgili Örnek Problemler
Pisagor Teoremi, dik üçgenlerle ilgili birçok problemde kullanılır. Aşağıda, Pisagor Teoremi’nin kullanıldığı birkaç örnek problem bulunmaktadır:
Örnek Problemler:
Problem 1: Bir dik üçgenin dik kenarları 3 birim ve 4 birim uzunluğundadır. Bu üçgenin hipotenüs uzunluğunu bulun.
Problem 2: Bir bahçenin köşelerinden birine dik açılı iki çit inşa ediliyor. Bir çit 8 metre uzunluğunda, diğer çit ise 15 metre uzunluğundadır. Köşeden köşeye çitin uzunluğunu bulun.
Problem 3: Bir merdivenin birinci basamağına 6 adım uzaklıktaki bir lamba, merdivenin ikinci basamağına 8 adım uzaklıktadadır. Lambaya doğrudan çıkan bir kablo ne kadar olmalıdır?
Pisagor Teoremi, bu tür dik üçgen problemlerini çözmek için kullanışlı bir araçtır. Bu örnek problemler, Pisagor Teoremi’nin günlük hayattaki uygulamalarını anlamak için harika bir fırsat sunar. Bu teoremi kullanarak, farklı senaryolarda pratik yaparak konunun daha iyi anlaşılmasını sağlayabilirsiniz.
Pisagor Teoremi Kanıtları
Pisagor Teoremi’nin kanıtları, bu matematiksel ilkenin geçerliliğini ve doğruluğunu göstermek için kullanılır. Pisagor Teoremi’nin kanıtları arasında geometric proof (geometrik kanıt), algebraic proof (cebirsel kanıt) ve visual proof (görsel kanıt) yöntemleri bulunmaktadır. Bu kanıtlar, Pisagor Teoremi’nin her durumda geçerli olduğunu ortaya koymak için kullanılır.
Geometric Proof (Geometrik Kanıt):
Pisagor Teoremi’nin en eski kanıt şeklidir. Genellikle karelerin alanları ve şekillerin iç içe geçmesiyle gösterilir. Üçgenin kenarlarına kareler çizilir ve bu karelerin alanları karşılaştırılarak teoremin doğruluğu kanıtlanır.
Algebraic Proof (Cebirsel Kanıt):
Bu kanıt şekli, Pisagor Teoremi’nin cebirsel denklemlerle ispatlanmasını içerir. Üçgenin kenar uzunlukları kullanılarak yapılan cebirsel manipülasyonlarla teoremin doğruluğu kanıtlanır.
Visual Proof (Görsel Kanıt):
Bu kanıt, geometrik şekillerin düzgün bir şekilde gösterilmesiyle Pisagor Teoremi’nin doğruluğunu gösterir. Örneğin, bir karenin kenarları kullanılarak teoremin doğruluğu görsel olarak kanıtlanabilir.
Pisagor Teoremi’nin bu farklı kanıt şekilleri, matematiksel problemleri çözerken ve geometrik ilişkileri anlarken büyük ölçüde yardımcı olmaktadır. Bu kanıtlar, teoremin derinliğini anlamak ve matematiksel düşünme becerilerini geliştirmek için oldukça önemlidir.
Pisagor Teoremi Uygulamaları
Pisagor Teoremi’nin matematikten günlük hayata birçok uygulaması bulunmaktadır. Bu teorem, farklı alanlarda kullanılarak çeşitli problemlere çözüm olabilmektedir. İşte Pisagor Teoremi’nin bazı uygulama alanları:
İnşaat Mühendisliği: Yapılarda kullanılan dikdörtgen biçimindeki yapı elemanlarının kenar uzunluklarının hesaplanması ve yapıların stabilitesinin belirlenmesinde Pisagor Teoremi aktif olarak kullanılır.
Coğrafya: Harita üzerindeki mesafelerin ve koordinatların hesaplanmasında Pisagor Teoremi’nin uygulamaları bulunmaktadır.
Bilgisayar Bilimi: Bilgisayar grafikleri ve programlamada, özellikle geometrik hesaplamalarda Pisagor Teoremi’nin formülü sıkça kullanılır.
Mimari: Bina planlarının çiziminde, odaların ve mobilyaların yerleştirilmesinde simetrik düzenlemeler için Pisagor Teoremi kullanılır.
Pisagor Teoremi, temel matematik bilgisinin ötesinde, günlük hayatta ve farklı mesleklerde karşımıza çıkan pek çok problemde çözüm sunmaktadır. Bu nedenle teoremin uygulamalarını anlamak, pratik hayatta da faydalı olacaktır.
Pisagor Teoremi’nin Faydaları
Pisagor Teoremi matematik dünyasında geniş bir kullanım alanına sahiptir ve birçok faydası bulunmaktadır. Pisagor Teoremi’nin faydaları arasında şunlar bulunmaktadır:
Geometri Problemlerinin Çözümü: Pisagor Teoremi, dik üçgenlerin kenar uzunluklarını bulmak için kullanılır. Bu sayede geometri problemlerini çözmek daha kolay hale gelir.
İnşaat ve Mimarlık: İnşaat ve mimarlık alanında Pisagor Teoremi, doğru açılı köşelerin kontrol edilmesi ve dik açılı üçgenlerin oluşturulması için kullanılır. Böylece binaların ve yapıların sağlam temeller üzerine inşa edilmesi sağlanır.
Navigasyon: Denizciler ve pilotlar, Pisagor Teoremi’ni kullanarak rotalarını planlar ve mesafeleri hesaplar. Bu sayede seyir güvenliği ve doğru mesafe hesaplamaları yapılır.
Bilgisayar Grafikleri: Bilgisayar grafikleri ve oyun geliştirme alanında Pisagor Teoremi, 3 boyutlu uzayda nesnelerin konumlarının belirlenmesinde ve perspektif hesaplamalarında kullanılır.
Pisagor Teoremi’nin bu faydaları, matematiksel düşünme becerilerinin günlük yaşamda ve endüstrideki uygulamalarını vurgular. Bu teoremin anlaşılması ve kullanılması, birçok alanda karşımıza çıkan problemleri çözmek için güçlü bir araç oluşturur.
Sıkça Sorulan Sorular
Pisagor Teoremi nedir?
Pisagor Teoremi, dik üçgenlerin kenarları arasındaki ilişkiyi tanımlayan bir geometrik teoremdir. Bu teorem, A kenarı a, B kenarı b ve C kenarı c olan dik üçgenlerde, a^2 + b^2 = c^2 formülüyle ifade edilir.
Pisagor Teoremi kim tarafından bulunmuştur?
Pisagor Teoremi, Antik Yunan matematikçisi Pisagor tarafından bulunmuştur. Bu nedenle adını Pisagor’dan almıştır.
Pisagor Teoremi nerede kullanılır?
Pisagor Teoremi, geometri, trigonometri, mühendislik, fizik, ve bilgisayar bilimleri gibi birçok alanda kullanılan temel bir teoremdir. Özellikle kenar uzunlukları arasındaki ilişkiyi hesaplarken ve alan hesaplamalarında sıkça kullanılır.
Pisagor Teoremi hangi durumlar için geçerlidir?
Pisagor Teoremi, sadece dik üçgenler için geçerlidir. Dik üçgen, bir açısı 90 dereceden büyük olmayan üçgen olarak tanımlanır ve yalnızca bu tip üçgenler için Pisagor Teoremi uygulanabilir.




